Problem#
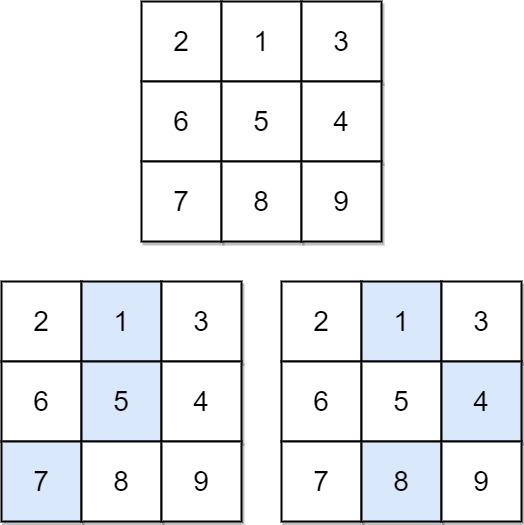
給你一個 nxn 的陣列,問你從上面走到最下面最短路徑總和為多少?
可以左右斜著走,但只能往下走,意即對於位置 $(i, j)$ 可以往 $(i+1, j-1)$ (左下), $(i+1, j)$ (下方), $(i+1, j-1)$ (右下) 走
想法#
對於起點 $(i, j)$ 可以往三個方向走,令 $f(i, j) = 最短路徑總和$ 則可以給出 $f(i, j) = min(f(i+1, j-1), f(i+1, j), f(i+1, j+1))$,接著加上 dp 表格用於記憶化搜索
- 時間複雜度: $\mathcal{O}(n^2)$
- 空間複雜度: $\mathcal{O}(n^2)$
AC Code#
top-down dp
賞析#
心得#
原本直覺暴力枚舉第一排 DFS ($\mathcal{O}(n^3)$) 會過,但後來看題解要 dp QQ
看來 leetcode 測資都給很多