Problem#
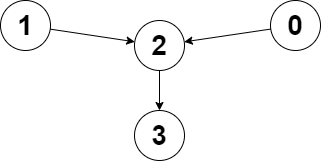
給你一個有 $n$ 個點的有向圖,每個點只有一條邊,並且給你兩個整數 node1 和 node2,要你回傳一個 node i (node1 和 node2 都到得了) ,其 index 使得 “node1 到 node i 的距離” 和 “node2 到 node i 的距離” 的最大值越小越好
如果有多種解,回傳 index 最小的即可;無解回傳 -1。
- 測資限制:
- $2 \le n \le 10^5$
edge.size() = n- 可能有出現環,但一定沒有自環
1 | edges = [2,2,3,-1] |
想法#
從 node1 和 node2 各自 dfs 一次,記錄各自的以該點為起始點對於所有點的"距離 array" dis[],接著枚舉 i=0~n 找 max(node1_dis[i], node2_dis[i]) 的最小值,紀錄 index 回傳 (dis[i] = -1 代表無法到達 i 點,在找最小值時要忽略)
- 時間複雜度: $\mathcal{O}(n)$
- dfs: $\mathcal{O}(V+E) = \mathcal{O}(n+n)$, 枚舉: $\mathcal{O}(n)$
- 空間複雜度: $\mathcal{O}(n)$
AC Code#
心得#
- 題目 input 的
edges其實就是圖了(adjacency matrix) 下意識轉成 adjacency list 導致多花 100ms