Leetcode 787 - Cheapest Flights Within K Stops

題目

Problem#

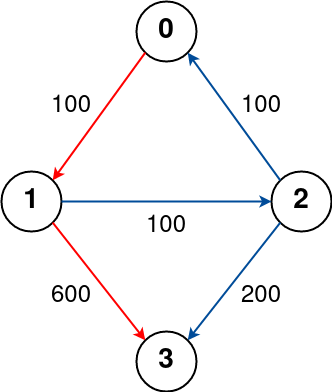
有 $n$ 座城市由 flights[i] = [fromi, toi, pricei] 個班機來往，給你起始點src和結束點dst以及整數 k (代表最多停留 k 個城市)，問你最便宜要花多少錢，如果沒有這種路徑則回傳 -1。

• 測資限制:
  • $1 \le n \le 100$
  • $0 \le flights.length \le (n * (n - 1) / 2)$

想法#

dijkstra 但不儲存 distance 改儲存 depth (路徑長度)，也因為每次都挑最小的費用的 node 所以當 current node = dst 時會是最小費。

• 時間複雜度: $\mathcal{O}(EK\log{EK})$
  • 每個 edge 要處理 k 次，每次 push/pop heap $\mathcal{O}(n\log{n})$
• 空間複雜度: $\mathcal{O}(N+EK)$
  • $\mathcal{O}(EK)$ : pq 數量

AC Code#

賞析#

TODO: BFS, bellman ford

心得#

一開始我沒想到是要多維護路徑長 (k) 看解答才想到QQ