Problem#
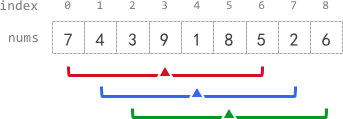
給你一個整數陣列 nums 有 $n$ 個數字,和一個整數 $k$。對於 index $i$ 能覆蓋 $[i-k, i+k]$ 範圍,其範圍內的平均數為 $avg[i]$ 問你能不能求出這個陣列
如果涵蓋的範圍比 $n$ 大 ($2 \times k + 1 > n$) 或是其中超出 n 的 index ($i < 0$ or $i \ge n$),則該 $avg[i] = -1$
測資限制#
- $1 \le n \le 10^5$
- $0 \le \text{nums}[i], k \le 10^5$
想法#
可以枚舉每個 $i$ 直接去算範圍總和,然後求平均 $\mathcal{O}(n^2)$。求總和可以用前綴和(prefix sum),則複雜度可以在 $\mathcal{O}(n)$
- 時間複雜度: $\mathcal{O}(n)$
- 空間複雜度: $\mathcal{O}(n)$
AC Code#
賞析#
官方題解是雙指標去求總和 & 平均數,然後每次向右就加上最右邊的、減去最左邊的 時間$\mathcal{O}(n)$,空間$\mathcal{O}(1)$