Problem#
給你一個陣列 nums和一個非負整數 k,你可以做以下操作
- 挑一個數字 $nums[i]$ 其中 $i \in [0, n-1]$
- 將 $nums[i]$ 換成 $[nums[i] - k, nums[i] + k]$ 其中的數字
定義一個 array 的美麗值(Beauty)為「相同數字」的最長子序列,問你回傳最大的 beauty 值為多少?
注意: 對於每個 index 只能執行一次操作
測資限制#
- $1 \le n \le 10^5$
- $0 \le nums[i], k \le 10^5$
想法#
將 $nums[i]$ 和其 $+k, -k$ 的範圍畫在數線上,可以發現最大的 beauty 值會出現在線段覆蓋最多的地方,所以此題其實是線段覆蓋問題
naive: 對每個數字 $nums[i]$ 去掃過一次 $[nums[i] - k, nums[i] + k]$ 統計覆蓋範圍,掃完之後再去掃一次統計的陣列去看最大數字是多少 $O(nk)$ TLE
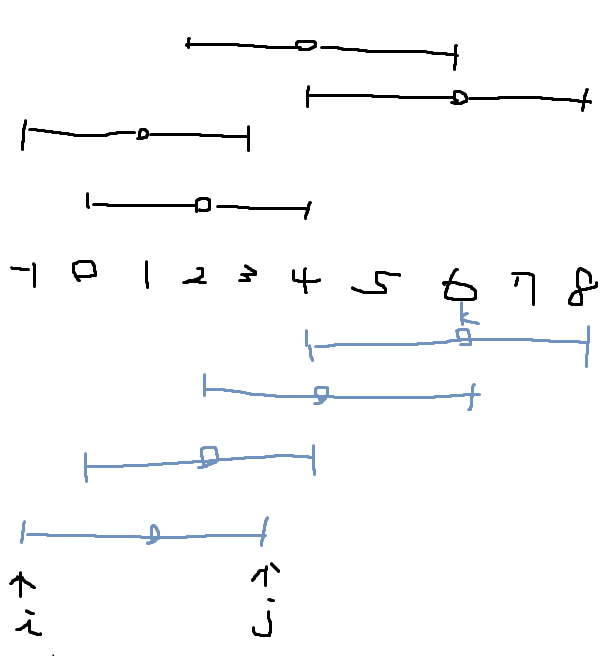
先 sort 一遍 nums,然後建出 nums[i]-k, nums[i]+k 的陣列,然後雙指標,去看左界的數字有沒有小於等於右界的數字,如果是的話則代表要挑那個範圍(cur++);反之代表當前數字超過右界,要反選那個範圍(cur--)。
為什麼?: 如果左界(a[i])在右界(b[j])的右邊,則代表在挑 a[i] 之前,要先反選 b[j] 的區間,因為在數字 a[i] 時 a[j], b[j] 的區間並沒有覆蓋到,所以要反選。 (看第一個範例,當 i=3, j=1 時)
跑完所有左界就夠了,因為我們目標是找最大的 beauty 值,跑完所有右界就只會越來越小而已,對於答案並沒有幫助。
- 時間複雜度: $\mathcal{O}(n\log{n})$
- 空間複雜度: $\mathcal{O}(n)$
AC Code#
賞析#
TODO: 官方題解
心得#
一開始都只想出 $O(n^2)$ 的作法,有想到可以用區間覆蓋解,但是沒想到 $O(n\log{n})$ 的方法QQ