Problem#
你能操縱一個西洋棋的騎士(Knight)旗子,它只能走 L 字形。
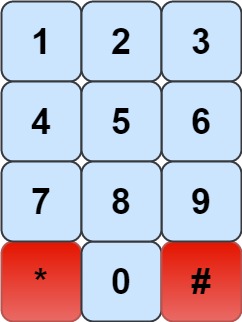
有一個數字鍵盤,從 0 到 9 是可以走的格子,* 和 # 不能走,你只能照騎士的走法去走去組合電話號碼,給你一個數字 n 代表電話號碼長度,問你能不能回傳最多有幾種不同電話號碼組合?
測資限制#
- $1 \le n \le 5000$
- 移動總共 n-1 次
- 答案可能很大要 mod $10^9+7$
想法#
先從 n = 1 開始想,每個格子的可能的走法是以下情況:
1 | // n = 1 |
接著試著求出 n = 2 的組合數,以 1 號格子為例,可以到達它的是 6 號和 8 號格子:
- 到達
6號格子有 $3$ 種方法,從6到1有 $1$ 種方法 - 到達
8號格子有 $2$ 種方法,從8到1有 $1$ 種方法 - 那從路徑
6 -> 1或8 -> 1總共就是 $3+2$ 種方法
可以用此規律求出從 0 到 9 的長度 2 有幾種方法。可以得出: 下個狀態($i+1$)就是從上個狀態($i$)加總可以到達第 $j \in [0, 9]$ 號格子的方法數。
1 | // n = 2 |
AC Code#
- 時間複雜度: $\mathcal{O}(n)$
- 空間複雜度: $\mathcal{O}(1)$
可以將狀態第二個外度壓縮在兩層就好,每次做完在將後蓋前。
賞析#
官方題解竟然有線代的解法