Problem#
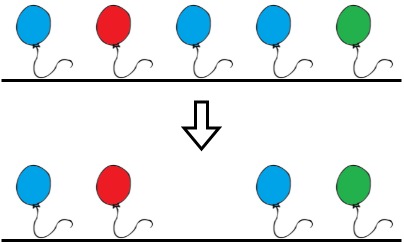
有 $n$ 個氣球,每個氣球是 color[i] 顏色,顏色不能連續出現,如果有相鄰的顏色的話,可以花 neededTime[i] 戳破第 $i$ 個氣球。
問你總共最小要花多少時間讓所有氣球的顏色不連續?
測資限制#
- $1 \le n \le 10^5$
- $1 \le t \le 10^4$
想法#
雙指標,找到相同顏色的氣球連續出現的區間
naive: 找到連續的區間,接著去加總 size-1 個氣球花費的時間
improve: 對於一個連續的區間,改成找最大的數字,所花費的時間 = 總和 - 最大的數字
AC Code#
- 時間複雜度: $\mathcal{O}(n)$
- 空間複雜度: $\mathcal{O}(1)$
心得#
一開始沒想到刪到剩下一個相當於: 找最大接著總和減去最大=除了最大之外的數字總和(戳破的氣球),反而去找小的