Problem#
給你 $m \times n$ 的二維陣列 grid 裡面只包含 0 和 1,你可以對每行、列進行 flip 操作(0 變 1,1 變 0),每列可以組成一個 binary 數字,最後加總起來就是分數,你可以 flip 無限次(或不 flip),問你最大的分數是多少。
測資限制#
- $1 \le m, n \le 20$
想法#
貪心
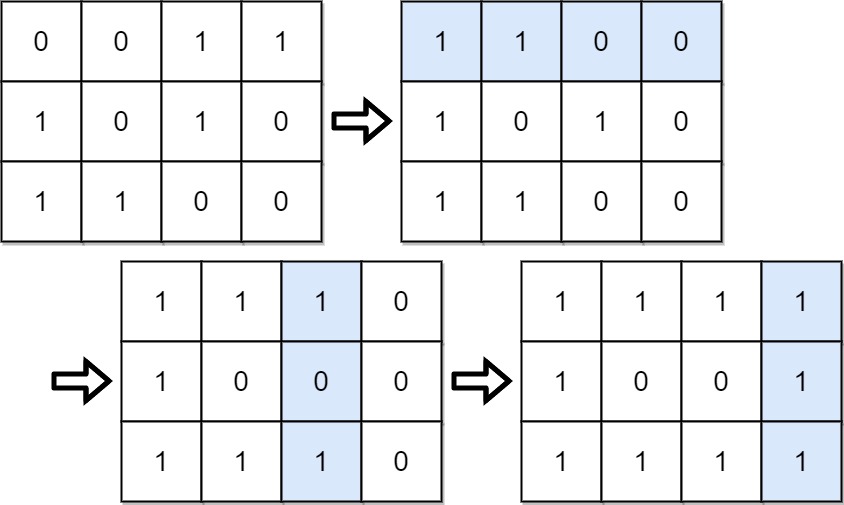
目標要找最大,所以最左邊的 bit 一定要是 1,如果有一列的最左 bit 是 0 的話,就 flip 整列。接著剩下的行,就看 0 與 1 的數量,目標是所有 1 的數量都要「大於等於」 0 的數量,所以遇到 1 的數量小於 0 的數量的行,就 flip 該行,如此一來便是最大的數字。
加總 $m$ 列即是答案。
AC Code#
- 時間複雜度: $\mathcal{O}(mn)$
- 空間複雜度: $\mathcal{O}(1)$